| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 광주인공지능학원
- 웹크롤링
- python
- 인공지능
- 파이썬
- iris붓꽃
- 데이터프레임
- 스마트인재개발원
- Selenium
- 크롤링
- CountVectorizer
- 인공지능학원
- 댓글분석
- 활성화함수
- 광주국비지원학원
- 유투브크롤링
- jsp
- tfidf
- 자바
- 과대적합제어
- permisision부여
- DataFrame
- sellenium
- 딥러닝
- 과대적합
- 머신러닝
- relu
- servlet
- 토큰화
- 셀리니움
- Today
- Total
+ Hello +
[광주인공지능학원] 딥러닝 활성화 함수 본문
import numpy as np
import matplotlib.pyplot as plt1. 활성화 함수
- 신경망은 선형회귀와 달리 한 계층의 신호를 다음 계층으로 그대로 전달하지 않고 비선형적인 활성화 함수를 거친 후에 전달한다
-> 신경망을 모방하여 사람처럼 사고하는 인공지능 기술을 구현하기 위함
- 입력에 일정 값을 곱해서 출력값을 결정하는 것(실제 신경망의 동작을 모방)
- 종류 : step function, sigmoid, tanh, relu
1) step function : 계단함수
- 0보다 크면 1이고 그렇지 않으면 0인 함수
def step_function(x):
return np.array(x>0, dtype =np.int)
x =np.arange(-5.0, 5.0, 0.1)
y=step_function(x)
plt.plot(x,y)
2) sigmoid 함수
def sigmoid_function(x):
return 1/(1+np.exp(-x))
x= np.arange(-5.0, 5.0, 0.1)
y=sigmoid_function(x)
plt.plot(x,y)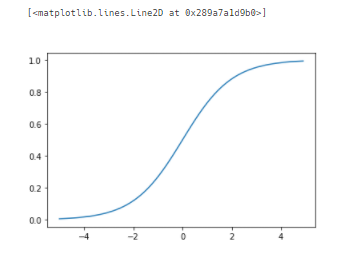
2-1) sigmoid 함수 미분
def d_sigmoid_funciton(x):
return sigmoid_function(x) * (1-sigmoid_function(x))
x = np.arange(-5.0, 5.0, 0.1)
y = d_sigmoid_funciton(x)
plt.plot(x,y)

* Step과 Sigmoid의 차이
- 선형 모델이 학습하기 위해서 경사하강법(cost 함수를 미분)을 사용

* 중간층에 활성화 함수로 비선형 함수를 사용하는 이유
- 계단 함수와 시그모이드 함수는 비선형 함수
- 활성화 함수로 선형함수(linear) ex) h(x) = cx를 사용하면 중간층(은닉층)을 여러 개 구성한 효과를 살릴 수 없다
3) tanh(하이퍼볼릭 탄젠트)
x = np.arange(-5.0, 5.0, 1)
y = np.tanh(x)
plt.plot(x,y)

4) relu
relu는 미분하면 0 이하의 값은 0 나옴 그 이상의 값은 1이 나옴
- 미분 값이 1 나오기 때문에 기울기 소실의 문제가 발생하지 않음
- 기울기 소실을 해결
def relu_function(x):
# 0보다 작으면 0, 0보다 크면 원래 값을 그대로 출력
return np.maxium(x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu_function(x)
plt.plot(x,y)
* 딥러닝이 처음 등장했을 때 3가지 문제
- 과대적합 > dropout으로 해결(일부 파라미터만 사용)
- 기울기 소실 > relu로 해결
- 연산량 증가 > 그래픽 카드의 성능
2. 비용함수
- 분류 : 교차엔트로피오차(CEE)
- 회귀 : 평균제곱오차(MSE)
def mean_squared_error_function(y, t):
return np.sum((y-t) **2)
# 정답 레이블과 예측값이 일치하는 경우
t = np.array([0, 0, 1, 0, 0, 0,0, 0, 0, 0])
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
print(mean_squared_error_function(y,t))
- y : 실제값
- t : 예측값
3. 교차 엔트로피 오차 (CEE) : 분류

def cross_entropy_error_function(y,t):
# log값에서 y=0이면 log값이 무한대가 됨
# 아주 작은 값을 더해줌
return - np.sum(t*np.log(y))
# 정답 레이블과 예측값이 일치하는 경우
t = np.array([0, 0, 1, 0, 0, 0,0, 0, 0, 0])
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
print(mean_squared_error_function(y,t))
위 과정은 스마트인재개발원 수업 내용입니다.
'+ 스마트인재개발원 +' 카테고리의 다른 글
| [광주인공지능학원] CNN 개, 고양이 분류 (1) | 2021.08.16 |
|---|---|
| [광주인공지능학원] 딥러닝 과대적합 제어 (1) | 2021.08.09 |
| [광주인공지능학원] 딥러닝 손글씨 분류하기 (1) | 2021.07.29 |
| [광주 인공지능학원] 딥러닝 개요 (1) | 2021.07.26 |
| [광주 인공지능학원] 안드로이드 Activity & Intent (1) | 2021.07.26 |




